Jump Game

经典题目了属于

leetcode 55

给定一个非负整数数组 nums ，你最初位于数组的第一个下标。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标。

子问题是,看能不能跳到i位置,i位置跳不到,后面的必定更跳不到
由于初始站在索引0位置,所以0位置是可以跳到的.dp[0] = nums[0]
dp[i] 表示子数组[0,i]内可跳的最远的位置
当索引到k,分两种情况:

k > dp[k - 1], 则此k索引位置不可达,后面更不能到达,退出返回false
更新dp[k]后,若dp[k]已经包含最大索引,则返回true

JavaScript代码如下：

var canJump = function (nums) {
    // if (nums.length === 1) {
    //     return true;
    // }
    let dp = Array(nums.length).fill(0);
    dp[0] += nums[0];
    let i = 1;
    for (; i < nums.length; i++) {
        if (i > dp[i - 1]) {
            console.log('此时 i 为 ', i);
            return false;
        }
        dp[i] = Math.max((i + nums[i]), dp[i - 1]);
        console.log(dp[i]);
        if (dp[i] >= nums.length - 1) {
            return true;
        }
    }
    // 只有一个元素的情况直接返回true
    return true
};

Jump Game II

leetcode 45

给定一个非负整数数组nums，初始时，你还是站在数组第一个元素位置。
元素的值表示在此元素位置可以跳的最大距离
你的目标是以最小的跳跃次数到达最后一个元素
你可以假设总能到达最后一个元素。

中文版的官方题解，解法一，贪心：

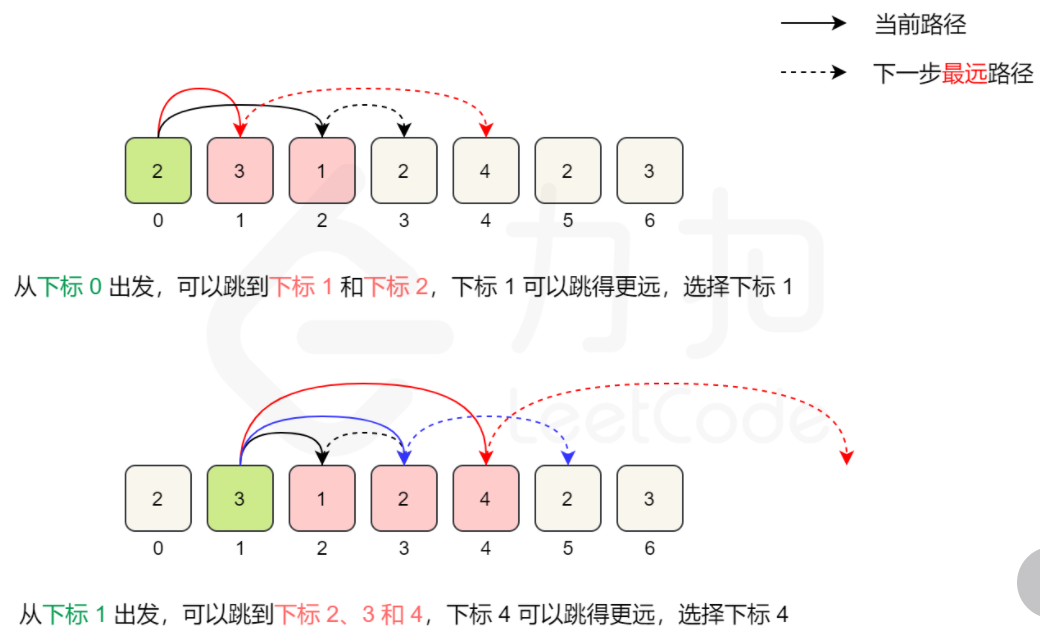
如果有多个位置通过跳跃都能够到达最后一个位置，那么我们应该如何进行选择呢？
贪心

从最后一步向前查找,找哪一个元素可以一步到达最后一个元素
需要从左向右查找,这样才能找到距离最后一个元素最远的位置,
继续贪心地寻找倒数第二步跳跃前所在的位置，以此类推，直到找到数组的开始位置。

var jump1 = function (nums) {
    let position = nums.length - 1;
    let step = 0;
    while (position > 0) {
        for (let i = 0; i < position; i++) {
            if (i + nums[i] >= position) {
                position = i;
                step += 1;
                break;
            }
        }
    }
    return step;
};

时间复杂度：当数组全是1时，显然是On
空间复杂度：O1

中文版的官方题解，解法二，贪心：

正向查找：

索引i遍历数组
使用一个变量跟踪当前索引i位置可以到达的最大的索引位置。
当i索引到达此位置时，step就加1。

    let step = 0;
    let maxPos = 0;
    let end = 0;  //边界,索引到达边界时更新步数和边界
    for (let i = 0; i < nums.length - 1; i += 1) {
        maxPos = Math.max(maxPos, nums[i] + i);
        console.log('maxPos', maxPos);
        // 边界内有更远的跳跃距离?那也得建立在这个元素在之前的跳跃距离内这个前提下
        // 所以,需要步数加1和更新边界
        if (i === end) {
            end = maxPos;
            step += 1;
        }
        console.log(step, i);
    }
    console.log(step);
    return step;

不同路径II-leetcode63

一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为“Start” ）。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/unique-paths-ii
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

动态规划解法：

var uniquePathsWithObstacles = function(obstacleGrid) {
    let m = obstacleGrid.length;
    let n = obstacleGrid[0].length;
    let dp = Array.from(Array(m)).map(() => Array(n).fill(0));
    for(let i=0; i<m; i++) {
        // 有障碍物，则后面的不可达
        if (obstacleGrid[i][0] === 1) {
            break;
        }
        dp[i][0] = 1;
    }
    for(let i=0; i< n; i++) {
         // 有障碍物，则后面的不可达
        if (obstacleGrid[0][i] === 1) {
            break;
        }
        dp[0][i] = 1;
    }
    for(let i=1; i<m; i++) {
        for(let j=1; j< n; j++) {
            if (obstacleGrid[i][j] === 1) { // 有障碍物，则不可达
                dp[i][j] = 0;
            } else {
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }            
        }
    }
    return dp[m-1][n-1];
};

没啥好说的，就是leetcode62 不同路径加了几个判断。

动态规划系列2